Index of Refraction of Air
Jack A. Stone and Jay H. Zimmerman I. Introduction This web page can be used to calculate the refractive index of air for a given wavelength of light and given atmospheric conditions (air temperature, pressure, and humidity). The web page also calculates the wavelength in ambient air, λ, from the vacuum wavelength λvac and the refractive index n, through the relationship |   | (1) | It is the wavelength in air that determines the basic length scale of measurements performed with laser interferometers. This page is intended to serve as an aid to people doing interferometry who wish to check their own calculations of the refractive index against this NIST calculation. At present the web page calculates only the standard index of refraction (the phase index); certain modulated-light, multi-frequency, or pulsed-laser applications require the group index to properly account for the effects of the atmosphere. The following text discusses some issues relevant to the calculation of index of refraction, provides guidance relating to the input parameters on the web page, and discusses the uncertainty of the results. Various points on the web page shown in blue hypertext are linked to relevant sections of this article. II. Edlén or Ciddor? Guidance in Choosing the Equation Two basic methods for calculating the refractive index are available here--an equation developed by Ciddor1 and an updated version of the Edlén equation2,3,4 as modified by Birch and Downs and with an additional modification of our own. We suggest that, unless you are an expert in the field with a specific reason to choose one equation over the other, there is no need to worry about the small differences between the two equations--you can choose either one and need not read any further. The Birch and Downs version of the Edlén equation is probably the most commonly used equation for calculating index of refraction of air for precision measurements at temperatures near 20 °C (68 °F). A very similar equation has been developed by Bonsch and Potulski5. Ciddor1 and Rüeger6 have argued that the equation derived by Ciddor should give somewhat better results than Birch and Downs over a broader range of wavelengths and under extreme environmental conditions of temperature, pressure, and humidity. For this reason the Ciddor equation has been adopted by the International Association of Geodesy (IAG) as the standard equation for calculating index of refraction; the equation is believed to provide more accurate results under the more extreme temperature and humidity conditions of interest for geodetic surveying. In fact, the Edlén equation includes approximations for the water vapor term that are only accurate near 20 °C, and consequently the equation can be in error at high temperature and humidity. When temperatures approach 35 °C and high humidity is present, the Birch/Downs/Edlén equation will clearly not give as good results as does Ciddor. (Under these circumstances the Birch/Downs/Edlén equation may not even be superior to the much-simplified version of the Edlén equation given in Appendix B.) When the temperature increases to 50 °C with 100 % humidity, this error in the Birch/Downs/Edlén water vapor term rises to 5×10-7. However, a very simple improvement of the water-vapor term, as described in Section III. Comments Regarding the Calculations, eliminates most of the differences between Birch/Downs/Edlén and the Ciddor equation at high temperature and humidity. As can be seen in Section III, after this modification of the Birch/Downs/Edlén equation, in almost all circumstances of practical interest the differences between the two equations are small relative to the basic uncertainty of the equations. This result gives us good confidence in the two equations at the quoted level of uncertainty except under extreme conditions. Furthermore, it is difficult to imagine the realistic need for ultra-precision measurements, requiring an accuracy in the refractive index better than a few parts in 107, under the extreme environmental conditions where the two equations differ by more than 1 part in 107 (such as at -40 °C, or at +65 °C with 100 % humidity at 633 nm wavelength). Note that there have been no direct experimental measurements to support either equation under these environmental extremes. Nevertheless, under some circumstances the Ciddor equation might be expected to give marginally better results, because it has been developed with broader applicability in mind (based very directly on BIPM density equation of reference 10) and it arguably treats the dispersion more accurately.
 |
|  | III. Comments Regarding the Calculations For a detailed explanation of the Edlén equation, see Appendix A and references 2, 3 and 4. It is important to note that for the calculations on this web page we use a slight modification of the water vapor term given by Birch and Downs in reference 4. The water vapor term, equation (3) of reference 4, is written in a temperature-independent form and hence is only valid at temperatures very near 19.6 °C (the temperature at which the constants were fitted7). When dealing with temperatures much different from 19.6 °C, the accuracy of the water vapor term can be significantly improved if it is multiplied by the ratio 292.75/(t+273.15), where t is the Celsius temperature, so as to account for the change in density with changing temperature (in the ideal gas approximation). The modified version of the water vapor correction (Birch/Downs equation 3), is then | 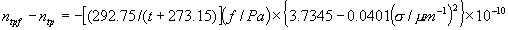  | (2) | where (ntpf - ntp) is the water vapor correction, f is the partial pressure of water vapor, and σ is the wave number. This equation is written using the notation and symbols of Birch and Downs. We use a different notation in the rest of this article. Rewritten in our notation, equation (2) appears in Appendix A as equation (A49). This modification of the Birch and Downs formula eliminates most of the discrepancy between the Birch and Downs formulation and the calculations of Ciddor at high temperature and humidity. For a detailed explanation of the Ciddor Equation, see reference 1 and Appendix A. Our calculation differs from Ciddor only in two minor aspects. First, we use a slightly different method to calculate saturation vapor pressure (to relate dew point temperature to mole fraction). Second, we use the 1998 CODATA value for the molar gas constant (see equation A30). The resulting disagreements in the refractive index are only a few parts in 1010. See the discussion of Humidity in Section IV and see Section V, Calculating Saturation Vapor Pressure. IV. Comments Regarding Inputs to the Equations Vacuum Wavelength The web page will accept input values for vacuum wavelength ranging from 300 nm to 1700 nm, the range of validity proposed by Ciddor. (Birch and Downs claim a range of validity only from 350 nm to 650 nm, but this range can be extended with little concern, except possibly under very high humidity conditions.) Note that the visible region extends from approximately 400 nm to 700 nm (0.4 µm to 0.7 µm). The standard red helium-neon laser, used for many metrology applications, has a wavelength in vacuum that is within a few parts in 106 of 632.991 nm. Infrared diode lasers commonly operate at wavelengths ranging from the visible up to 1600 nm or beyond. Pressure Atmospheric pressure may be expressed in a variety of common pressure units. In SI units, the web page accepts inputs ranging from 10 kPa to 140 kPa, but a warning is issued if the pressure falls outside of the more realistic range from 60 kPa to 120 kPa. There is no reason to doubt the validity of the equations at least over the range 60 kPa to 120 kPa, although Ciddor's suggested lower pressure limit (80 kPa) is slightly higher than suggested here (and is perhaps unnecessarily restrictive for work at high elevation). Standard atmospheric pressure at sea level is conventionally taken to be 101.325 kPa (approximately 760 mm Hg). Temperature Air temperature may be expressed in either Celsius or Fahrenheit. The web page will accept temperatures within the range of validity suggested by Ciddor, -40 °C to +100 °C (-40 °F to 212 °F). CO2 Concentration For all but the most accurate calculations, the CO2 concentration can be taken to be 450 parts in 106 by volume. In the literature on index of refraction, carbon dioxide concentration is universally expressed in "parts per million" or "ppm," meaning parts in 106. The use of "parts per million" and "ppm" is now discouraged. One possible alternative to "ppm" is micromole per mole (µmol/mol). 450 µmol/mol is a conventionally accepted value for CO2 concentration recommended by Birch and Downs as characteristic of concentrations encountered in closed rooms. This value is somewhat higher than typical concentrations encountered outdoors, but CO2 levels are unlikely to ever drop significantly below 300 µmol/mol outdoors and may sometimes exceed 600 µmol/mol in a laboratory, so the suggested 450 µmol/mol is probably a reasonable compromise. Variations in CO2 concentration up to 150 µmol/mol away from the suggested value have only a very small effect (about 2×10-8) on index of refraction and can be ignored by most users. Using the web page, the CO2 content cannot be changed from its default value of 450 µmol/mol when using the Edlén equation, but it can be set to any value between 0 µmol/mol and 2000 µmol/mol when using the Ciddor equation.
 |
|  | Humidity Humidity can be specified by entering relative humidity (0 % to 100 %), dew point, frost point (analogous to dew point but for water vapor in equilibrium over ice), or partial pressure of water vapor. The web page will flag as suspect any humidity input that corresponds to a mole fraction of water vapor exceeding 20 % or corresponding to a relative humidity in excess of 85 % (where there is a potential for formation of water droplets in the air). A detailed discussion of humidity calculations follows below. The discussion is included so as to provide detailed background information but it can be safely ignored by most users of this web page. We convert from one representation of humidity to another as shown in equations (3) through (8) below. These formulae are used by Ciddor and by Birch and Downs in their calculations. We must caution the reader that equations (3) and (4) are not quite in accord with accepted representations of humidity, because they ignore the enhancement factor (a factor which accounts for the non-ideal behavior of a mixture of water vapor and dry air). The Birch and Down equation expresses humidity in terms of partial pressure of water vapor. Given the dew point (or frost point) td, we convert to partial pressure pv using |   | (3) | where psv(td) is the saturation vapor pressure at the dew point (or at the frost point if appropriate). Partial pressure of water vapor is calculated from fractional humidity h using | 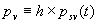  | (4) | where psv(t) is the saturation vapor pressure at the air temperature t. Note: If relative humidity RH is given in percent, ranging numerically from 0 to 100, then the fractional humidity h is | 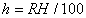  | (5) | Ciddor also makes implicit use of equations (3) and (4) for calculations in his paper where he compares his results to Birch and Downs, but his reliance on (3) and (4) is only incidental; his computation of the index of refraction is expressed in terms of the mole fraction of water vapor rather than in terms of partial pressure. For the Ciddor equation, we calculate the mole fraction from dew point, fractional humidity, or partial pressure of water vapor using equations (6), (7), and (8): where xv is the mole fraction of water vapor, f(p,t) is the enhancement factor at the air temperature t and air pressure p, and td is the dew point (or frost point). Equations (6) and (7) are standard equations for calculating mole fraction from dew point or relative humidity (see, for example, reference 10). Ciddor must also calculate mole fraction from partial pressure, and he appears to do this with equation (8), although his paper is slightly ambiguous on this point. Equations (3) and (4) are not quit consistent with (6) and (7); they lead to different expressions for the fractional humidity that differ from each other by the ratio f(p,t)/f(p,td). As a practical matter this factor is of negligible importance; the ratio is so close to unity that it affects the calculated index of refraction only at a level below 3×10-9 for temperatures below 50 °C. The Edlén equation totally ignores the enhancement factor and other non-ideal gas effects (variations in the compressibility Z) relating to water vapor. Although in principle this approach is incomplete, it is a good approximation because variations in f and Z are small under typically encountered environmental conditions and have little effect if they are consistently ignored in all of the analysis, including the analysis used to determine the water vapor term in the formula for index of refraction. At high temperatures and 100 % humidity, variations of f and Z away from their values at 20 °C (where the water vapor term was analyzed7) might cause minor errors in the humidity correction, but we estimate that any such errors do not exceed 1×10-8 for temperatures below 50 °C and are less than 4×10-9 for temperatures below 40 °C. Further details of the humidity calculations are given in Appendix A. V. Calculating Saturation Vapor Pressure We calculate the saturation vapor pressure using the equations recommended by the International Association for the Properties of Water and Steam (IAPWS) and described by Huang in reference 9. (See Huang's equations 4 an 8, which are also given here in Appendix A, Section A-I, Saturation Vapor Pressure.) By contrast, Ciddor1 and Bonsch and Potulski5 use formulae given by Davis10 and Giacomo8. The differences between the two methods of calculation are entirely negligible for our purposes; the difference in saturation vapor pressure does not exceed 0.4 kPa for temperatures between 0 °C and 40 °C, changing the index of refraction by less than 2×10-10. At higher temperatures the differences in the calculated saturation vapor pressure are only slightly more substantial, increasing to 34 kPa at 100 °C, which would shift the index of refraction by roughly 1×10-8. We use the IAPWS formulation because it is generally accepted as the best formula available. The estimated uncertainty of the IAPWS equation is 20 kPa at 100 °C but decreases rapidly to less than 2 kPa at 45 °C and 0.7 kPa at 20 °C. For temperatures below 0 °C, it is necessary to specify whether vapor pressure over ice [Huang's equation (8)] or over water [Huang's equation (4)] is to be calculated. The web page allows the user to enter either dew point (for vapor-water equilibrium) or frost point (for vapor-ice equilibrium). When relative humidity is input, the calculation of psv(t) assumes vapor-water equilibrium when the air temperature is above 0 °C and vapor-ice equilibrium below 0 °C. VI. Uncertainty and Range of Validity Please note carefully: almost all significant errors in determining the index of refraction come not from uncertainty in the Ciddor or modified Edlén equations but from inaccuracy in measurement of atmospheric parameters, most notably air temperature and pressure. Measurement errors that could produce an error of 1×10-6 (1 part per million) in the index of refraction (hence a length-proportional error of 1 part in 106) include: - an error of 1 °C (1.8 °F) in air temperature
- an error of 0.4 kPa (3 mm Hg) in air pressure
- an error of 50 % in relative humidity at sufficiently high air temperatures (near 35 °C)
The uncertainty shown on the web page is only the intrinsic uncertainty of the equations themselves, exclusive of the (potentially much more important) measurement errors. A detailed discussion of this intrinsic uncertainty is given below. The uncertainty of the equations is difficult to assess with confidence, but some guidance is provided by references 1 and 4. In reference 4, Birch and Downs state: "The 3 σ uncertainty associated with these equations is ±3×10-8 (mainly due to uncertainties in pressure, temperature and humidity measurement) and applies to ambient atmospheric conditions over the range of wavelengths from 350 to 650 nm". They do not define "ambient atmospheric conditions". Under normal conditions encountered in a dimensional measurement laboratory, the uncertainty estimate of Birch and Downs has been confirmed by the measurements of Bonsch and Potulski5. As discussed elsewhere in this paper, the Birch and Downs equation does not achieve the ±3×10-8 accuracy under extreme environmental conditions, and has particular problems at high temperature and humidity unless the water vapor term is modified as described in Section III. In reference 1 Ciddor gives a more conservative estimate of the uncertainty, but claims a larger range of validity. He states: "One cannot expect, therefore, an overall uncertainty of better than 2-5×10-8 " where he is referring to uncertainty "at the 1 σ level." For the range of validity, he suggests "-40 °C to +100 °C, 80 kPa to 120 kPa, and 0 % to 100 % humidity...over the wavelength range from approximately 300 nm to 1690 nm". There is perhaps another implicit restriction in this range; one might not expect the formula to maintain its full accuracy at the high end of Ciddor's temperature and humidity ranges, where the mole fraction of water vapor becomes large. Also, when relative humidity is high--above 80 % or 90 %--it is possible for water droplets to form in the air and degrade the accuracy of the computed index of refraction.6 The pressure range given by Ciddor appears to be unnecessarily restrictive at low pressures that might be encountered when doing measurements at high elevations. In conclusion, we estimate that under typical laboratory atmospheric conditions the relative expanded uncertainty (coverage factor k=2) of both equations is about 2×10-8. Based on Ciddor's uncertainty estimate, we assume that the expanded uncertainty of his equation increases to as much as 1×10-7 for extreme conditions that are far from standard conditions. In addition, we feel it is appropriate to further increase Ciddor's uncertainty when water vapor partial pressure is very high, in order to account for uncertainty in the refractivity of water vapor. We estimate this uncertainty based on the independent water vapor measurements at 633 nm of Birch and Downs7, Beers and Doiron11, and Bonsch and Potulski5. The first two of these investigations gave nearly the same result, while the measurements of Bonsch and Potulski give an answer that differs by 7×10-12 per Pascal of vapor pressure. This represents a difference in the index of refraction of less than 1×10-8 over the range of conditions where the water vapor term was actually measured, but the discrepancy grows to 7×10-8 at 45 °C and 100 % humidity. We assign as a rough estimate of the expanded uncertainty of the water vapor correction a value of 8×10-12 per Pascal of vapor pressure, equal to twice the standard deviation of the three water vapor measurements at 633 nm, and add it in quadrature to other uncertainty contributions. This may somewhat underestimate the water vapor uncertainty at both long and short wavelengths. Lack of experimental evidence makes it difficult to estimate the uncertainty for wavelengths longer than 650 nm. At short wavelengths--below 400 nm--the dispersion formulae of the modified Edlén and Ciddor equations differ by as much as 6×10-12 per Pascal of vapor pressure, and there is only minimal experimental evidence in support of one equation relative to the other. Rather than making a judgment as to which expression for the water vapor dispersion is more accurate, we add in quadrature an additional uncertainty term, proportional to vapor pressure and to 1/λ4, that is approximately equal to the difference between the two equations. An empirical equation for the uncertainty that attempts to quantify all the statements made here is given in equation (A50) of Appendix A, Section A-V, Uncertainty. To asses the validity of the modified Edlén equation far from standard temperature and pressure, we assume (with minimal supporting evidence) that the Ciddor equation is more reliable than Edlén under these conditions and, consequently, that discrepancies between the two equations arise primarily from inaccuracy in the modified Edlén equation. We account for this additional uncertainty in the Edlén equation by increasing its estimated uncertainty so as to account for the discrepancy with Ciddor, as shown in equation (A51) of Section A-V. We also add in quadrature an uncertainty of 2×10-8 to account for deviations of CO2 concentration from the assumed 450 µmol/mol by as much as ±150 µmol/mol. This expanded uncertainty for uncorrected CO2 is estimated roughly on the basis of graphical data presented in reference 12 showing measured CO2 concentrations in industrial settings. Note that higher CO2 concentrations might be encountered in poorly ventilated surroundings7. Also note that solvent vapors might significantly alter the index of refraction in a poorly ventilated environment.
 |
|  | VII. Comparison of Ciddor and Modified Edlén Equations For dry air in the expected range of validity of the Ciddor equation (60 kPa to 120 kPa, -40 °C to 100 °C, and wavelength between 300 nm and 1700 nm), differences in the two equations are largest at the very low temperature (-40 °C) and high pressure (120kPa). Here the difference between Edlén and Ciddor ranges from 1.4×10-7 at a wavelength of 1700 nm to 1.6×10-7 at 300 nm. These differences are probably well below anything of practical interest under such extreme conditions. Over a more restricted range, for dry air at temperatures between 5 °C and 40 °C, pressures between 60 kPa and 110 kPa, and wavelengths between 300 nm and 1700 nm, the maximum difference between the Ciddor and modified Edlén equations does not exceed 1×10-8, significantly less than the claimed uncertainties of the equations. At 100 % humidity, the maximum difference within this range increases to 8×10-8, with the maximum error occurring at high humidity (100 % at 40 °C), high pressure (110 kPa), and short wavelength (300 nm). This discrepancy arises from differences in the water vapor dispersion at the shortest wavelengths; for wavelengths longer than 400 nm, the maximum discrepancy over this range of atmospheric conditions is only 2.7×10-8. Table 1 shows a comparison of the Ciddor and modified Edlén equations under various circumstances, calculated using this web site. The water vapor partial pressure or mole fraction was calculated using equations (4) and (7) in conjunction with the IAPWS vapor pressure formulae (see Table 2). | Temperature (Celsius) | Relative Humidity (%) | Pressure (kPa) | Wavelength (nm) | Index of Refraction (Ciddor) | Index of Refraction (Modified Edlén) | Difference ×108 (Ciddor-Edlén) | | 20 | 0 | 101.325 | 633 | 1.000271800 | 1.000271799 | 0.1 | | 20 | 0 | 60 | 633 | 1.000160924 | 1.000160920 | 0.4 | | 20 | 0 | 120 | 633 | 1.000321916 | 1.000321918 | -0.2 | | 50 | 0 | 100 | 633 | 1.000243285 | 1.000243270 | 1.5 | | 5 | 0 | 100 | 633 | 1.000282756 | 1.000282750 | 0.6 | | -40 | 0 | 100 | 633 | 1.000337580 | 1.000337471 | 10.9 | | 50 | 100 | 120 | 633 | 1.000287924 | 1.000287864 | 6.0 | | 40 | 75 | 120 | 633 | 1.000299418 | 1.000299406 | 1.2 | | 20 | 100 | 100 | 633 | 1.000267394 | 1.000267394 | 0.0 | | 40 | 100 | 110 | 1700 | 1.000270247 | 1.000270237 | 1.0 | | 20 | 0 | 101.325 | 1700 | 1.000268479 | 1.000268483 | -0.4 | | 40 | 100 | 110 | 300 | 1.000289000 | 1.000288922 | 7.8 | | 20 | 0 | 101.325 | 300 | 1.000286581 | 1.000286579 | 0.2 | | -40 | 0 | 120 | 300 | 1.000427233 | 1.000427072 | 16.1 | | Table 1. Index of refraction as calculated using the Modified Edlén equation and Ciddor equation, assuming 450 µmol/mol CO2 concentration. The vapor pressure and mole fraction for 100 % humidity is calculated using the IAPWS equation. Values for the index given in the table have one or two significant figures more than can be realistically justified, as an aid to people wishing to check their own calculations against ours. | | Temperature (Celsius) | Saturation Vapor Pressure (Pa) | | 100 | 101418 | | 50 | 12351 | | 40 | 7384 | | 20 | 2339 | | -10 | 260 | | Table 2. Examples of saturation vapor pressure calculated using the IAPWS formulae. These numbers, which have been rounded off to the nearest Pascal, include the values needed for the calculations of Table 1. | VIII. Acknowledgments We give our thanks to Dr. Joseph T. Hodges of NIST for his patient explanations of humidity. IX. References 1. Phillip E. Ciddor, "Refractive index of air: new equations for the visible and near infrared," Appl. Optics 35, 1566-1573 (1996). 2. B. Edlén, "The refractive index of air," Metrologia 2, 71-80 (1966). 3. K.P. Birch and M.J. Downs, "An updated Edlén equation for the refractive index of air," Metrologia 30, 155-162 (1993). 4. K.P. Birch and M.J. Downs, "Correction to the updated Edlén equation for the refractive index of air," Metrologia 31, 315-316 (1994). 5. G. Bonsch and E. Potulski, "Measurement of the refractive index of air and comparison with modified Edlén's formulae," Metrologia 35, 133-139 (1998 ). 6. Jean M. Rüeger, "Refractive Index Formulae for electro-optical distance measurement," presented at the XXIst International Congress of Surveyors (FIG'98), 19-25 July 1998, Brighton, UK. Paper TS28/1 (1998). 7. K.P. Birch and M.J. Downs, "Precise determination of the refractive index of air," NPL Report number NPL-MOM-90, National Physical Laboratory, Teddington UK, Crown copyright 1988, Available from National Technical Information Service, Springfield, VA 22161 (1988 ). 8. P. Giacomo, "Equations for determination of the density of moist air (1981)," Metrologia 18, 33-40 (1982). 9. Peter H. Huang, "New equations for water vapor pressure in the temperature range -100 °C to 100 °C for use with the 1997 NIST/ASME steam tables," in Papers and abstracts from the third international symposium on humidity and moisture, Vol. 1, p. 69-76, National Physical Laboratory, Teddington, Middlesex, UK, April 1998. 10. R.S. Davis, "Equation for the determination of the density of moist air (1981/91)," Metrologia 29, 67-70 (1992). 11. J. Beers and T. Doiron, "Verification of revised water vapor correction to the refractive index of air," Metrologia 29, 315-316 (1992). 12. K.P. Birch, F. Reinboth, R.E. Ward, and G. Wilkening, "The effect of variations in the refractive index of industrial air upon the uncertainty of precision length measurement," Metrologia 30, 7-14 (1993). Appendix A: Summary of Computations Used on the Web Page Appendix A is intended to summarize all calculations used in the web site, in a manner that approximates a step-by-step cookbook explanation. The calculations are arranged in the order that they would be carried out--that is, each equation makes reference only to previously calculated quantities. A-I. Saturation Vapor Pressure When using either the Edlén or Ciddor equations, and when either relative humidity or dew point is known, it is necessary to calculate the saturation vapor pressure at a temperature t, where t is either the air temperature or the dew point temperature. We do this using the IAPWS formula as shown below, but it should be noted that the much simpler formula of Davis10 will also be entirely adequate for this task at temperatures above 0 °C. Follow the instructions below to calculate saturation vapor pressure using the IAPWS formula. (a) Convert temperature to the Celsius scale. In the following discussion the Celsius temperature is denoted t. (b) For saturation vapor pressure over water, use formulae (A1) to (A7) to calculate the saturation vapor pressure psv(t) with constants K1through K10 as shown in Table A1. | 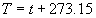  | (A1) | | 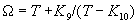  | (A2) | | 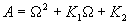  | (A3) | | 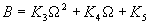  | (A4) | | 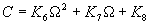  | (A5) | | 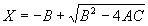  | (A6) | | 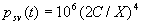  | (A7) | | Constant | Coefficient | | K1= | 1.16705214528E+03 | | K2= | -7.24213167032E+05 | | K3= | -1.70738469401E+01 | | K4= | 1.20208247025E+04 | | K5= | -3.23255503223E+06 | | K6= | 1.49151086135E+01 | | K7= | -4.82326573616E+03 | | K8= | 4.05113405421E+05 | | K9= | -2.38555575678E-01 | | K10= | 6.50175348448E+02 | | Table A1. Coefficients for calculating saturation vapor pressure, from reference 9. | (c) For saturation vapor pressure over ice, calculate psv(t) using equations (A8) through (A13): | 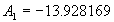  | (A8) | | 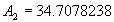  | (A9) | |   | (A10) | | 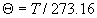  | (A11) | | 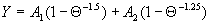  | (A12) | | 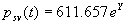  | (A13) | A-II. Determining Humidity (a) Humidity for Edlén Equation. When using the Edlén equation, humidity must be expressed as water vapor partial pressure. (a1) If partial pressure is given in units other than Pascal, convert to Pascal (a2) If you are given the dew point (or frost point) td, calculate partial pressure using | | 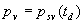  | (A14) | where psv(td) is calculated as shown previously in section A-I, using (A1) through (A7) for dew point or (A8) through (A13) for frost point. (a3) If you are given the relative humidity RH in percent (that is, the numerical value ranges from 0 to 100), calculate partial pressure using | | 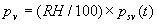  | (A15) | where t is air temperature and psv(t) is calculated using (A1) through (A7) when t>0 or using (A8) through (A13) for t<0. (b) Humidity for Ciddor Equation. When using the Ciddor equation it is necessary to express humidity as a mole fraction. (b1) First calculate the enhancement factor f using where p is the air pressure in Pascals and t is Celsius temperature (either air temperature or dew point temperature as required by the formula below). (b2) If you are given dew point td (or frost point) in degrees Celsius, and air pressure p in Pascals, calculate mole fraction xv using | |   | (A18) | (b3) If you are given relative humidity RH in percent (ranging numerically from 0 to 100), air pressure p (Pascals), and air temperature t, calculate the mole fraction xv using | | 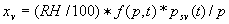  | (A19) | where psv(t) is calculated using (A1) through (A7) when t>0 or using (A8) through (A13) for t<0. (b4) If you are given partial pressure pv (Pascals), air pressure p (Pascals), and air temperature t (Celsius), calculate mole fraction xv using | | 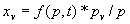  | (A20) | A-III. Ciddor Calculation of Index of Refraction (a) Preliminaries: - Convert all temperatures to Celsius.
- Convert all pressures to Pascal.
- Calculate the mole fraction xv as described previously.
(b) Define constants: | 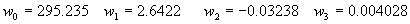  | (A21) | | 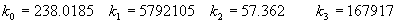  | (A22) | | 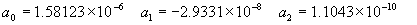  | (A23) | | 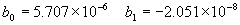  | (A24) | |   | (A25) | | 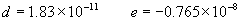  | (A26) | | 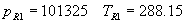  | (A27) | |   | (A28) | | 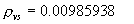  | (A29) | |   | (A30) | (c) Convert the laser vacuum wavelength λ to micrometers and then find | 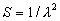  | (A31) | (d) Calculate intermediate results that depend on S: (e) Given the CO2 concentration xCO2 in µmol/mol, calculate (f) Find the Kelvin temperature, the compressibility, and density components: | 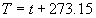  | (A36) | | 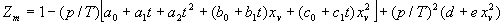  | (A37) | | 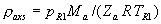  | (A38) | |   | (A39) | | 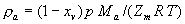  | (A40) | (g) Calculate the index of refraction n: |   | (A41) | A-IV. Edlén Calculation of the Index of Refraction (a) Preliminaries: - Convert all temperatures to Celsius.
- Convert all pressures to Pascal.
- Calculate partial pressure pv as described previously.
(b) Define constants: (c) Convert the laser vacuum wavelength λ to micrometers and then find | 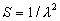  | (A45) | (d) Calculate intermediate results at air pressure p, water vapor partial pressure pv, and temperature t: (e) Calculate the final result for index of refraction n, using our variation of the water vapor term: | 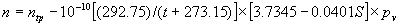  | (A49) | A-V. Uncertainty Equation (A50) below is an empirical equation that yields uncertainty estimates for the Ciddor equation that are consistent with Ciddor's uncertainty estimates at the extremes of the range of validity, reflect experimental evidence near normal atmospheric conditions that indicates a lower uncertainty is appropriate under these conditions, and is consistent with our estimated uncertainty of the water vapor term. (Note: do not change the number 273 in the formula to the apparently more accurate value of 273.15 or the accuracy of the formula will be degraded.) |   | (A50) | where UCiddor is the expanded (k=2) uncertainty, air pressure p and water vapor partial pressure pv are expressed in Pascals, temperature t is in Celsius, and wavelength λ is expressed in micrometers. The equation should not be misinterpreted as having any deep significance--it is no more than a computational tool--an interpolation formula--that empirically is found to be consistent with all statements made above and provides a means for interpolating between the uncertainty at normal laboratory conditions and at extreme conditions. In addition, the formula contains a factor of [p/(t+273)] so that the uncertainty decreases with decreasing air density; this factor insures that the relative uncertainty in the refractivity approaches a constant as the pressure approaches zero, as would be expected. (The refractivity r = n-1 is proportional to air density.) The formula allows us to plausibly assign an approximate numeric value to the uncertainty reported on the web page. For the uncertainty of the Edlén equation, we add in quadrature three terms: (1) the uncertainty of the Ciddor equation, (2) an uncertainty of 2×10-8 to account for potential variations of approximately ±150 µmol/mol in CO2 concentration away from 450 µmol/mol, the assumed value that remains fixed in our version of the Edlén equation, and (3) an additional term that is approximately equal to the difference between the Ciddor and Edlén equations far from normal laboratory temperature and pressure, based on our belief that Ciddor is arguably more accurate. The uncertainty is then given by | 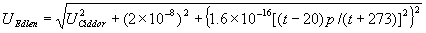  | (A51) | where the symbols have the same meaning as in (A50). Appendix B: Simple Shop-floor Formula for Refractive Index of Air We briefly mention an approximate formula that might be helpful for shop-floor work where only a hand calculator is available. One of several possible simplified equations for calculating index of refraction is |   | (B1) | where p is pressure in kPa, t is temperature in Celsius, and RH is relative humidity in percent (that is, ranging from 0 to 100). This formula is only valid for the standard, red He-Ne laser wavelength of approximately 633 nm, but this is not a serious limitation since 633 nm He-Ne lasers are used almost universally for displacement interferometry. The equation is expected to be accurate within an estimated expanded uncertainty of 1.5×10-7 (in common parlence, this might be expressed as 0.15 parts per million where "parts per million" means parts in 106) for temperatures between 0 °C and 35 °C, pressures 50 kPa to 120 kPa, humidity 0 % to 100 %, and CO2 concentration between 300 µmol/mol and 600 µmol/mol. Over this broad range of conditions, the simplified formula is comparable in accuracy to the Birch and Downs version of the Edlén equation, but not as accurate as the Ciddor equation or as the version of the Edlén equation given in this paper. Over a more limited range of conditions characteristic of metrology laboratories near sea level (temperature between 19.5 °C and 20.5 °C, pressure from 90 kPa to 110 kPa, 0 % to 70 % humidity, and CO2 concentration between 350 µmol/mol and 550 µmol/mol) this equation agrees with the Ciddor equation and with our version of the Edlén equation within 5×10-8 (0.05 parts per million). |